Homework #5

Due: June 1 (Thursday)

Problem: Construct arithmetic expression trees from either postfix or infix expressions.

Complete the skeleton class SyntaxTree.java and TreeBuilder.java shown below:

You must use the accompanied binary tree implementation located in cse2010.hw5.tree. The package contains link-based, tree-related classes discussed in lecture. The codes are almost identical to the ones in the textbook. The test code, LinkedBinaryTreeTest will help you understand how some core methods are used.

public class TreeBuilder {
    private static Map<String, Integer> operators = new HashMap<>();
    static {
        // We will consider only four binary operators: *, /, +, -
        operators.put("(", 1);
        operators.put("*", 1);
        operators.put("/", 1);
        operators.put("+", 1);
        operators.put("-", 1);
        operators.put(")", 1);
        // you may put other entry/entries if needed ...
    }

    private static Stack<SyntaxTree> operandStack = new Stack<>();
    private static Stack<String> operatorStack = new Stack<>();

    /**
     * Construct a syntax free from postfix arithmetic expression.
     */
    public static SyntaxTree buildFromPostfix(String expression) {
        initStacks();

        /**
         * You code goes here ...
         */

        return new SyntaxTree();
    }

    /**
     * Construct a syntax free from infix arithmetic expression.
     */
    public static SyntaxTree buildFromInfix(String expression) {
        initStacks();

        /**
         * You code goes here ...
         */

        return null;
    }

    private static void initStacks() {
        operandStack.clear();
        operatorStack.clear();
    }
}

The TreeBuilder provides two construction methods: buildFromInfix and buildFromPostfix. Constructing a syntax tree from a postfix expression is relatively straight-forward. But, it maybe (very) hard to construct it from an infix expression. So, you’d better start with buildFromPostfix first.
The Map is a simple data structure that stores (name, value) pairs. We can retrieve a value from the Map using key like this: For this homework, the key is the operator symbol and the value is the operator’s precedence.
```
private static Map<String, Integer> operators = new HashMap<>();
...
operators.put("(", 7);
...
int precedence = operators.get("(");  // null if not found
...
```

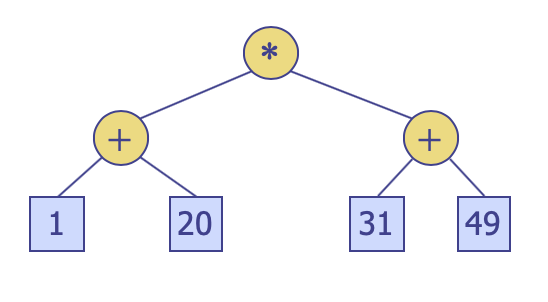
buildFromPostfix constructs an expression tree from a postfix expression.
```
SyntaxTree tree = SyntaxTree.buildFromPostfix("1 20 + 31 49 + *");
```
will generate tree like this
- Use TreeUtil.parse() to parse the expression and generate an array of string tokens from it.
```
// expression = "1 20 + 31 49 + *"
String[] tokens = parse(expression); // [1, 20, +, 31, 49, +, *]
```
- All operators and operands are stored as String in each tree node as an element.
- Only four binary operators (*, /, +, -) need to be supported.
- Each operand is a single letter string or an integer represented as string, possibly with multiple digits.
- If you need Stack, you can use the stack defined in Java’s collection library (java.util.Stack). Note that the java.util.Stack uses peek() instead of top().
buildFromInfix constructs an expression tree from an infix expression. All the codes below
```
SyntaxTree tree = SyntaxTree.buildFromInfix("(1 + 20) * (31 + 49)");
SyntaxTree tree = SyntaxTree.buildFromInfix("((1 + 20) * (31 + 49))");
```
will generate the same tree as above figure.
- The same guidelines given for buildFromPostfix also apply here. TreeUtil.parse() can still be used to parse the infix expression and generate an array of string tokens from it.
```
// expression = "(x + 20) * (y + 49)"
String[] tokens = parse(expression); // [(, x, +, 20, ), *, (, y, +, 49, )]
```
* Operator precedence is crucial when we construct syntax trees from infix expressions. Especially, “(” and “)” also need to be considered as operators when builing trees from infix expressions. * You must define operator’s precedence properly. * You can define additional operator constants, if needed. * Hint: One or more operators’ precedence(s) need to be changed whether it is (or they are) inside the operator stack or not.

As for the SyntaxTree class, you need to define one public evaluate method, and two private toInfix and indentTree methods.

public class SyntaxTree extends LinkedBinaryTree<String> {

    /**
     * Evaluate syntax tree.
     */
    public double evaluate() {
        /**
         * Your code goes here ...
         */
        return 0d;
    }

    /**
     * Returns postfix expression corresponding to this syntax tree.
     */
    public String toPostFix() {
        return cvtToString(postOrder());
    }

    /**
     * Returns prefix expression corresponding to this syntax tree.
     */
    public String toPreFix() {
        return cvtToString(preOrder());
    }

    /**
     * Returns fully parenthesized infix expression corresponding to this syntax tree.
     */
    public String toInfix() {
        return toInfix(root());
    }

    /**
     * Returns fully parenthesized infix expression corresponding to this syntax subtree.
     */
    private String toInfix(Position<String> position) {
        /**
         * Your code goes here ...
         */
        return null;
    }

    /**
     * Returns a formatted string representation of tree hierarchy.
     * The formatted string representation of the expression tree corresponsing
     * to {@code (a + b) * (c - d)} looks as follow:
     * *
     *   +
     *     a
     *     b
     *   -
     *     c
     *     d
     */
    public String showTree() {
        return indentTree(root(), 0);
    }

    /**
     * Returns a formatted string representation of the subtree hierarchy.
     * @param level indentation level; 0 means no indentation; the unit of
     *              the indentation level is two spaces.
     */
    private String indentTree(Position<String> position, int level) {
        Node<String> node = validate(position);
        StringBuilder builder = new StringBuilder();

        /**
         * You code goes here...
         */

        return builder.toString();
    }

    /**
     * Convert list of Positions to a serialized string in which
     * each element of the position is delimited by the ' ' character.
     */
    private String cvtToString(List<Position<String>> positions) {
        return positions.stream().map(Position::getElement).collect(Collectors.joining(" "));
    }
}

toInfix should generate fully parenthesized infix expression of the tree.
```
tree.toInfix() ==> "((1 + 20) * (31 + 49))"
```
Note the spaces around each operator.
evaluate calculates the arithmetic expression represented by the tree. Of course, if you use letters to denote operands, the expression cannot be evaluated. (You may safely ignore this case.)
```
tree.evaluate() ==> "1680.0"
```
Evaluation should be performed as double arithmetic.

showTree prints the tree as properly indented depending on the depth of each node.

tree.showTree() ==> "*\n"
                  + "  +\n"
                  + "    1\n"
                  + "    20\n"
                  + "  +\n"
                  + "    31\n"
                  + "    49\n"

The root node has 0 indentation. Nodes at level i should be indented as much as depth * 2 spaces.

How to test?

If everything works fine, the test results may look something similar like below:

What to submit?

Your source files archived in .zip or .jar format.
- Subject: Homework#5, Section [A|B], 성명, 학번
- Email to your TA